
For many students in Grades 8 and up, the numbers and shapes they've learned about really start to come together when they are making and solving linear equations. This topic integrates ideas about algebra, geometry, and functions and can be difficult for many children—and adults!—to wrap their heads around. This article explains what a linear equation is and walks through different examples. Then it offers lesson ideas for introducing and developing the concept of linear equations in one variable to your students.
What Is a Linear Equation?
Just like any other equation, a linear equation is made up of two expressions set equal to each other. There are some key features common to all linear equations:
- A linear equation only has one or two variables.
- No variable in a linear equation is raised to a power greater than 1 or used as the denominator of a fraction.
- When you find pairs of values that make a linear equation true and plot those pairs on a coordinate grid, all of the points lie on the same line. The graph of a linear equation is a straight line.
A linear equation in two variables can be described as a linear relationship between x and y, that is, two variables in which the value of one of them (usually y) depends on the value of the other one (usually x). In this case, x is the independent variable, and y depends on it, so y is called the dependent variable.
Whether or not it's labeled x, the independent variable is usually plotted along the horizontal axis. Most linear equations are functions. In other words, for every value of x, there is only one corresponding value of y. When you assign a value to the independent variable, x, you can compute the value of the dependent variable, y. You can then plot the points named by each (x,y) pair on a coordinate grid.
Describing Linear Relationships
Students should already know that any two points determine a line. So graphing a linear equation in fact only requires finding two pairs of values and drawing a line through the points they describe. All other points on the line will provide values for x and y that satisfy the equation.
The graphs of linear equations are always lines. However, it is important to remember that not every point on the line that the equation describes will necessarily be a solution to the problem that the equation describes. For example, the problem may not make sense for negative numbers (say, if the independent variable is time) or very large numbers (say, numbers over 100 if the dependent variable is grade in class).
What Does a Linear Equation Look Like?
Example 1: distance = rate × time
In this equation, for any given steady rate, the relationship between distance and time will be linear. However, distance is usually expressed as a positive number, so most graphs of this relationship will only show points in the first quadrant. Notice that the direction of the line in the graph below is from bottom left to top right. Lines that tend in this direction have positive slope. A positive slope indicates that the values on both axes are increasing from left to right.
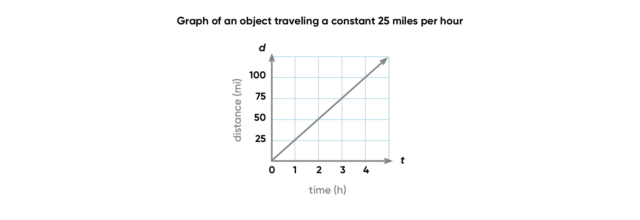
Example 2: amount of water in a leaky bucket = rate of leak × time
In this equation, since you won't ever have a negative amount of water in the bucket, the graph will show points only in the first quadrant. Notice that the direction of the line in this graph is top left to bottom right. Lines that tend in this direction have negative slope. A negative slope indicates that the values on the y-axis are decreasing as the values on the x-axis are increasing.

Example 3: number of angles of a polygon = number of sides of that polygon
Again in this graph, we are relating values that only make sense if they are positive, so we show points only in the first quadrant. Moreover, in this case, since no polygon has fewer than 3 sides or angles and the number of sides or angles of a polygon must be a whole number, we show the graph starting at (3,3) and indicate with a dashed line that points between those plotted are not relevant to the problem.
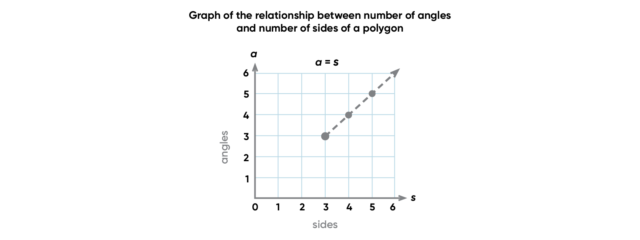
Example 4: degrees Celsius = 5/9 × (degrees Fahrenheit – 32)
Since it's perfectly reasonable to have both positive and negative temperatures, we plot the points on this graph on the full coordinate grid. (Although it's not visible on the graph, the lowest possible physical temperature is around –460° Fahrenheit, so not every solution on the graph is useful!)

Slope
The slope of a line tells two things: how steep the line is with respect to the y-axis and whether the line slopes up or down when you look at it from left to right. More technically speaking, slope tells you the rate at which the dependent variable is changing with respect to the change in the independent variable.
Calculating Slope
Pick any two points on the line. To find how fast y is changing, subtract the y value of the first point from the y value of the second point: (y2 – y1). To find how fast x is changing, subtract the x value of the first point from the x value of the second point: (x2 – x1). To find the rate at which y is changing with respect to the change in x, calculate the ratio: (y2 – y1)/(x2 – x1).
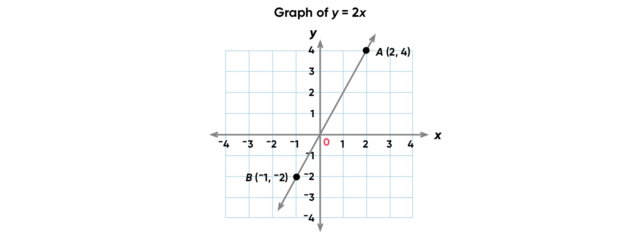
If we designate Point A as the first point and Point B as the second point, the slope of the line is (–2 – 4)/(–1 – 2) = –6/–3, or 2. It does not matter which points along the line you designate as A and B, just as long as we're consistent with which is the "first" point (x1,y1) and which is the "second" (x2,y2). If we designate Point B as the first point and Point A as the second point, the value of the slope is the same: (4 – -2)/(2 – -1) = 6/3 or 2. It is also the same value you will get if you choose any other pair of points on the line to compute slope.
Linear Equation Formula
The equation of a line can be written in a form that makes the slope obvious and allows you to draw the line without any computation. If students are comfortable with solving a simple two-step linear equation, they can write linear equations in slope-intercept form. The slope-intercept form of a linear equation is y = mx + b. In the equation, x and y are the variables. The numbers m and b give the slope of the line (m) and the value of y when x is 0 (b). The value of y when x is 0 is called the y-intercept because (0,y) is the point at which the line crosses the y-axis.
You can draw the line for an equation matching this linear formula by plotting (0,b), then using m to find another point. For example, if m is 1/2, you can interpret that as a difference in 1 among y coordinates for every difference in 2 among x coordinates (that is, (y2 – y1)/(x2 – x1) = 1/2). Count +2 on the x-axis, then +1 on the y-axis to get to another point: (2, b + 1).
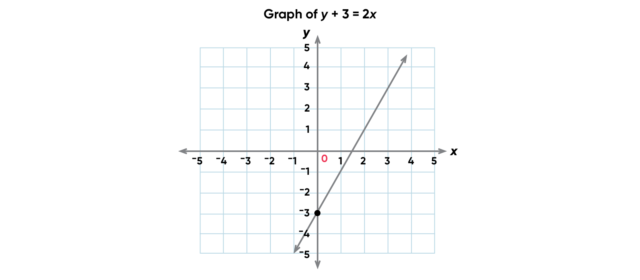
The equation for this line is y + 3 = 2x. In slope-intercept form, the equation is y = 2x – 3. In this form you can easily see that the slope m = 2. Looking at the graph, the slope really is 2 since for every +2 change in y, there is a +1 change in x. Now look at b in the equation: –3 should be where the line intercepts the y-axis, and it is.
Positive Slope
When a line slopes up from left to right, it has a positive slope. This means that a positive change in y is associated with a positive change in x. The steeper the slope, the greater the rate of change in y in relation to the change in x. A slope of 6 is steeper than a slope of 1, which is in turn steeper than a slope of 1/6. When the line represents real-world data points plotted on a coordinate plane, a positive slope indicates a positive correlation, and the steeper the slope, the stronger the positive correlation.
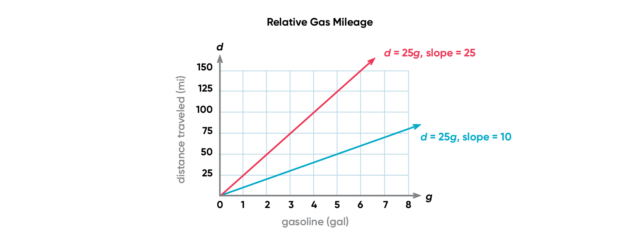
Consider a linear equation where the independent variable g is gallons of gas used and the dependent variable d is the distance traveled in miles. If you drive a big, old car, you get poor gas mileage. The amount of miles traveled is low relative to the amount of gas consumed, so the value m is a low number. The slope of the line is fairly gradual. If instead you drive a light, efficient car, you get better gas mileage. You travel more miles relative to the same amount of gas consumed, so the value of m is greater and the line is steeper. Both rates are positive because you still travel a positive number of miles for every gallon of gas you consume.
Negative Slope
When a line slopes down from left to right, it has a negative slope. This means that a negative change in y is associated with a positive change in x. When the line represents real-world data points plotted on a coordinate plane, a negative slope indicates a negative correlation, and the steeper the slope, the stronger the negative correlation.
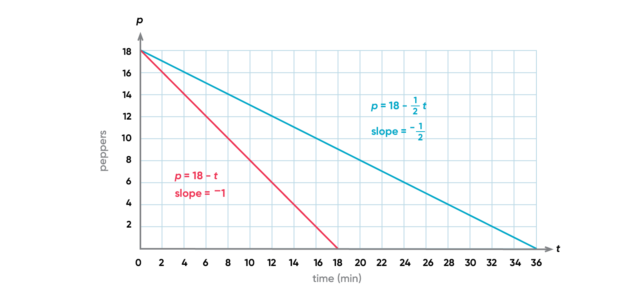
Consider a line that represents the number of peppers left to plant after minutes spent gardening. If the garden can fit 18 pepper plants, and you plant 1 pepper plant per minute, the rate at which the garden flat empties out is fairly high, so the absolute value of m is a greater number, and the line is steeper. If instead you only plant 1 pepper plant every 2 minutes, you still empty out the garden flat, but the rate at which you do so is lower. The absolute value of m is lower (1/2 instead of 1), and the line is not as steep.
Zero Slope
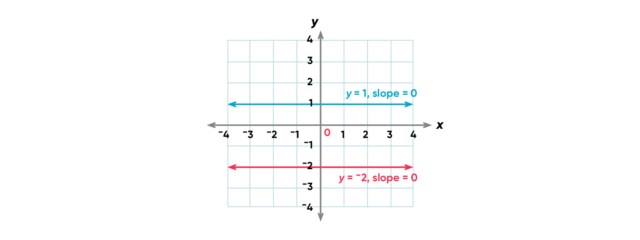
When there is no change in y as x changes, the graph of the line is horizontal. A horizontal line has a slope of zero.
Undefined Slope
When there is no change in x as y changes, the graph of the line is vertical. You cannot compute the slope of this line, because you would need to divide by 0. Notice how you can think of these lines as "infinitely steep," either positively or negatively. The slope of a vertical line is not defined.

Lines With the Same Slope
Two lines with the same slope have identical steepness. This means one of two things: either the lines are parallel or they're the same line.

In all three of these lines, every 1-unit change in y is associated with a 1-unit change in x. All three have a slope of 1.
Solving Two-Step Linear Equations with Rational Numbers
When a linear equation has two variables (as it usually does), it has an infinite number of solutions. Each solution is a pair of numbers (x,y) that make the equation true. Solving a linear equation usually means finding the value of y for a given value of x.
When the Equation Is Already in Slope-Intercept Form
If the equation is already in the form y = mx + b, with x and y variables and m and b rational numbers, solving for specific values is straightforward. Choose a value for x, and compute the corresponding value for y. You'll notice that an easy value to choose for x is 0, because in that case, y = b. Students may be asked to make tables of values for linear equations. These are simply T-tables with lists of values for x with corresponding values for y.
Two-step equations involve finding values for expressions that have more than one term. A term can be a number, a variable, or numbers and variables multiplied together. The terms in an expression are separated by addition or subtraction symbols. 2x is an expression with one term. 2x + 6 has two terms. To find a value for y given a value for x, substitute the x-value into the expression.
Consider the equation y = 2x + 6. Find the value for y when x = 5:
| Substitute the value for x into the equation. | y = 2(5) + 6 |
| Multiply. | y = 10 + 6 |
| Add. | y = 16 |
When the Equation Is Not in Slope-Intercept Form
When a linear equation is not in slope-intercept form (that is, not written as y = mx + b), students can still make a table of values to find solutions for the equation, but it may be simpler to put the equation in slope-intercept form first. This requires mirroring operations on each side of the equation until y is by itself on the one side of the equation, set equal to a linear expression involving x. You can manipulate the equation in this way because of equality properties:
- If a = b, then a + c = b + c.
- If a = b, then a – c = b – c.
- If a = b, then ac = bc.
- If a = b, then a ÷ c = b ÷ c (so long as c ≠ 0).
Consider 2x + y – 6 = 0. This equation is not in slope-intercept form, but you can use equality properties to get y on one side of the equation.
- You can subtract y from both sides of the equation to get 2x – 6 = –y. Then multiply both sides of the equation by –1 to get –2x + 6 = y.
- Alternatively, you can subtract 2x and add 6 to both sides of the equation to get y = –2x + 6.
The two equations, –2x + 6 = y and y = 6 – 2x are equivalent. You can turn one into the other by using the commutative property of addition, which states that a + b = b + a, and the symmetric property of equality, which states that if a = b, then b = a.
| Commutative Property of Addition | –2x + 6 = y is equivalent to 6 – 2x = y. |
| Symmetric Property of Equality | 6 – 2x = y is equivalent to y = 6 – 2x. |
Linear Equations: Introducing the Concept
Materials: Coordinate grid that all students can see (grid should go at least from –10 to +10 on both axes), tool to mark up the grid with points and lines
Preparation: Since students will be reading points from graphs and graphing lines from lists of points, they (and you) will need to be prepared to use a straightedge to generate accurate straight lines. If teaching online, use a digital tool capable of generating points and lines.
Prerequisite Skills and Concepts: Students need to be able to plot points on a coordinate plane and should be familiar with the various ways to indicate multiplication and division in an equation. They should also be familiar with the order of operations and the properties of equality.
- Carefully draw a line through (0,0) and (2,2) on the grid. Be sure to extend it in both directions so there are plenty of easy-to-name points on it.
- Say: Name some points on this line.
Students should come up with a list of the points named by integer coordinates. If not, spend some time naming points on a grid before continuing with this lesson. If students name non-integer points, such as (1.5,1.5), spend time explaining why those are on the line too. - Ask: Can you give me a rule for how to find y when we know x on this line?
Discuss how the coordinates are related, then ask students to write the rule in equation form. The equation for this line is y = x. - Say: That was the line for the equation y = x. How would you draw the line for the equation y = x + 3?
Have students independently try to draw the line. If feasible, have them pair up and compare their lines. Facilitate a discussion around the different lines students drew, highlighting similarities and differences. Then show one way of drawing the line: substitute some values for x into the equation, find the corresponding values for y, and then plot those coordinate pairs. Two points give you enough information to draw the line, but because mistakes are possible and human drawing isn't perfect, it is safer to generate at least three points. Display a T-table with the related x- and y-values, and draw the graph of the line. - Say: Now how would you draw the line for the equation y = 2x + 3?
Students are likely to use the strategy of making a T-table and computing points. If they forget to multiply their x-values by 2 before adding 3, remind them about the order of operations (multiply or divide left to right, then add or subtract left to right). Ask different students to generate different points, talking through their reasoning as they go. - Ask: Can someone give me a number between –5 and 5? Now, how about a number between –10 and 10?
Use these numbers to generate linear equations. The first number will be the coefficient of x, and the second will be added to the x term. Generate equations, find points, then draw the lines. You can make this activity more game-like by having students roll real or virtual number cubes. If you've been working with slope, these problems will give you a chance to reinforce that concept as well. (Ask: Do you think the slope of this line will be positive or negative? Do you think it will be very steep or not so steep? Will this line go through the origin?)
Linear Equations: Developing the Concept
Materials: Coordinate grid that all students can see (grid should go at least from –10 to +10 on both axes), tool to mark up the grid with points and lines
- Say When we generated points for lines in our last lesson, our equations always looked the same. In other words, they were always in the same form. Today, we'll look at different ways they might look.
- Say Can someone describe how to find some coordinate pairs for the linear equation, 2x + y = 15?
This is a two-step equation. Solutions involve assigning a value to x, then multiplying this value by 2 before trying to figure out what value of y would satisfy the equation. Students can use trial and error, or they can transform the equation using the equality properties:Write the equation. 2x + y = 15 Assign a value to x. 2(3) + y = 15 Multiply. 6 + y = 15 Subtract 6 from each side. 6 – 6 + y = 15 – 6 Subtract. y = 9 This solution gives us the point (3,9). Continue finding solutions, or coordinate pairs, for this equation until you are satisfied that students are comfortable with the process. Then, plot the points on your grid and draw the line.
Say Can someone describe how to find some points on the line described by the equation y + x/3 = 5?
Write the equation. y + x/3 = 5 Assign a value to x. y + 3/3 = 5 Divide. y + 1 = 5 Subtract 1 from each side. y + 1 – 1 = 5 – 1 Subtract. y = 4
This solution gives us the point (3,4). Students may notice that this doesn't look like previous linear equations. Explain that because x/3 is the same thing as (1/3)x, x/3 is still an ordinary term. Continue finding solutions, or coordinate pairs, for this equation until you are satisfied that students are comfortable with the process. Then, plot the points on your grid and draw the line.- Say Can someone describe how to find some points on the line described by the equation y – 6 = 2x?
Write the equation. y – 6 = 2x Assign a value to x. y – 6 = 2(3)
Multiply. y – 6 = 6 Add 6 to each side. y – 6 + 6 = 6 + 6 Add. y = 12 This solution gives us the point (3,12).
- By now, students should have noticed that an easy substitution for x is 0. This substitution will give you the point where the line crosses the y axis. Prompt students to come to this realization if they don't do so independently.
Assessment Hints
When students are solving multi-step equations, pay particular attention to whether they follow the order of operations. This is an important algebraic concept.
Also, watch for whether students really understand that the equality properties say that if you do something to one side of an equation, you MUST do the same thing to the other side of the equation. What you do is determined by the action indicated by the equation. If a number is subtracted from y and you want y to be by itself, add that number to each side of the equation and its opposite appears to 'move' to the other side of the equation. Similarly, if y is multiplied by a number, division will help you get y by itself.
***
Looking for a solution for students in Grades 5 and up that can help unlock learning for linear relationship equations and formulas and beyond? Explore Math 180, a revolutionary approach to math intervention.
Get our free Math Intervention eBook today.












