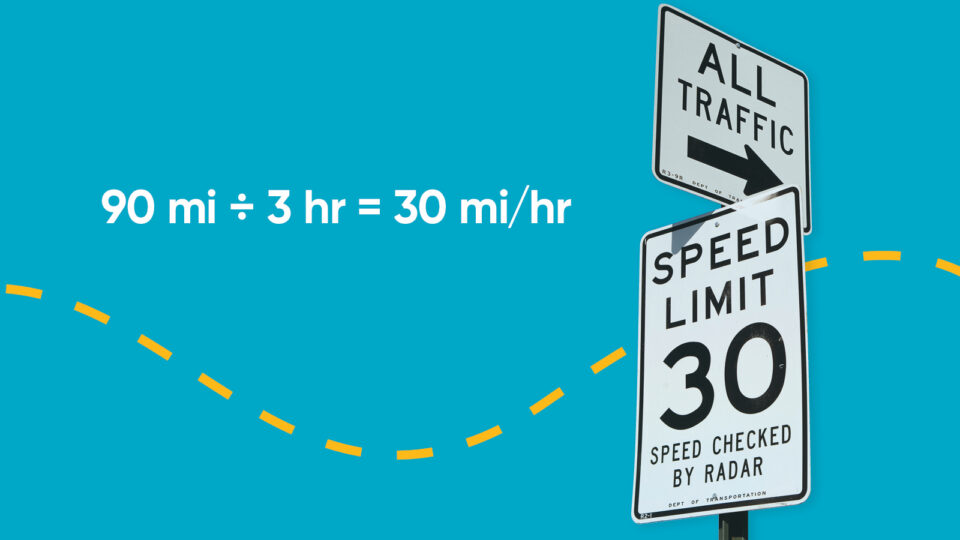
The heart of middle school mathematics, and a key part of algebra readiness, is understanding ratios and rates. The overview and lessons below are tools to prepare students, usually in Grades 6 and up, who are ready to learn about these concepts. The lessons below will typically cover two days of instruction.
Ratios and Rates
A ratio is a comparison of two numbers or measurements. The numbers or measurements being compared are sometimes called the terms of the ratio. For example, if a store sells 6 red shirts and 8 green shirts, the ratio of red to green shirts is 6 to 8. You can write this ratio as 6 red/8 green, 6 red:8 green—or when writing fast or trying to make a point—simply 6/8 or 6:8. Both expressions mean that there are 6 red shirts “for every” 8 green shirts. Notice how you can rewrite 6/8 as 3/4, no different from any other time a math concept can appear as a fraction.
A rate is a special ratio in which the two terms are in different units. For example, if a 12-ounce can of corn costs 69¢, the rate is 69¢ for 12 ounces. This is not a ratio of two like units, such as shirts. This is a ratio of two unlike units: cents and ounces. The first term of the ratio (69¢) is measured in cents, and the second term (12) in ounces. You can write this rate as 69¢/12 ounces or 69¢:12 ounces. Both expressions mean that you pay 69¢ “for every” 12 ounces of corn, and similar to the shirt ratio, can enter calculations as the fraction 69/12. But notice that this time, a new unit is created: cents per ounce.
Rates are used by people every day, such as when they work 40 hours per week or earn interest every year at a bank. When rates are expressed as a quantity of 1, such as 2 feet per second (that is, per 1 second) or 5 miles per hour (that is, per 1 hour), they can be defined as unit rates. You can write any rate as a unit rate by reducing the fraction so it has a 1 as the denominator or second term. As a unit rate example, you can show that the unit rate of 120 students for every 3 buses is 40 students per bus.
120/3 = 40/1
You could also find the unit rate by dividing the first term of the ratio by the second term.
120 ÷ 3 = 40
When a price is expressed as a quantity of 1, such as $25 per ticket or $0.89 per can, it is called a unit price. If you have a non-unit price, such as $5.50 for 5 pounds of potatoes, and want to find the unit price, divide the terms of the ratio.
$5.50 ÷ 5 pounds = $1.10 per pound
The unit price of potatoes that cost $5.50 for 5 pounds is $1.10 per pound.
Rates in the Real World
Rate and unit rate are used to solve many real-world problems. Look at the following problem. “Tonya works 60 hours every 3 weeks. At that rate, how many hours will she work in 12 weeks?” The problem tells you that Tonya works at the rate of 60 hours every 3 weeks. To find the number of hours she will work in 12 weeks, write a ratio equal to 60/3 that has a second term of 12.
60/3 = ?/12
60/3 = 240/12
Removing the units makes the calculation easier to see. However, it is important to remember the units when interpreting the new ratio.
Tonya will work 240 hours in 12 weeks.
You could also solve this problem by first finding the unit rate and multiplying it by 12.
60/3 = 20/1
20 × 12 = 240
When you find equal ratios, it is important to remember that if you multiply or divide one term of a ratio by a number, then you need to multiply or divide the other term by that same number.
Let's take a look at a problem that involves unit price. “A sign in a store says 3 Pens for $2.70. How much would 10 pens cost?” To solve the problem, find the unit price of the pens, then multiply by 10.
$2.70 ÷ 3 pens = $0.90 per pen
$0.90 × 10 pens = $9.00
Finding the cost of one unit enables you to find the cost of any number of units.
What Is a Unit Rate in Math?
Your students have no doubt encountered rates and ratios before (have they seen a speed limit sign?), but it may help them to review these concepts before solving problems that use them.
Standard: Understand the concept of a unit rate a/b associated with a ratio a:b with b ≠ 0. (6.RP.A.2)
Prerequisite Skills and Concepts: Students should have a basic understanding of ratios, how to write them, and an ability to simplify a ratio. Students should also have an ability to work with fractions and find equivalent fractions.
- Say: Today we are going to look at a special type of ratio called a rate. Does anyone know what I mean by a rate?
Students may say that a rate is a ratio in which the quantities being compared use different units such as dollars and ounces or miles and hours. Students may use common English synonyms for rate such as speed. If so, point out that speed means calculating how fast something is going by comparing distance to time, such as miles to hours. If necessary, explain what a rate is. - Say: Rates are commonly found in everyday life. The prices in grocery stores and department stores are often rates. Rates are also used in pricing gasoline or tickets, measuring speed, or paying hourly wages and monthly fees.
Have students think of other examples of rates. In addition to common real-world examples, encourage silly or unusual rates such as hip-hop artists per zip code or diamond collars per chihuahua. - Say: Two important ideas are unit rates and unit prices. What is the difference between rate and unit rate? Or price and unit price? Does anybody have any ideas?
Students will probably not know what a unit rate is, so provide them with the following explanation to explain rate vs. unit rate. - Say: A unit means one of something. A unit rate means a rate for one of something. We write this as a ratio with a denominator of one. For example, if you ran 70 yards in 10 seconds, you ran on average 7 yards in 1 second. Both of the ratios, 70 yards in 10 seconds and 7 yards in 1 second, are rates, but the 7 yards in 1 second is a unit rate.
- Ask: Now that you know what a unit rate is, what do you think a unit price is?
Students will say that it is the price of one item. If they don't, tell them what it is. - Ask: What is the unit price of 10 pounds of potatoes that costs $2.80?
Help students calculate that the unit price is $0.28 per pound by dividing the price by 10. - Share the following problem: “One store has carrots on sale for $1.14 for 3 pounds, while another store has carrots on sale for $0.78 for two pounds. Which store has the better deal?”
- Ask: What are we trying to find in this problem?
Students should say that we are trying to find out which is the better deal for carrots when thinking about the cost of each carrot. - Ask: What would help us find the better deal?
Students should say that if we find the unit price for the carrots at each store, we would know which was the better deal. - Say: Find the unit prices for the carrots at both stores and then we will discuss what you did.
Have students independently calculate the unit price and answer which store has the better deal. Compare how different students did the calculations, and have students discuss similarities and differences among the models they used and solutions they found. Allow for varying answers such as “the second store had the better deal for me because I would only want two carrots anyway.” If time permits, have students solve the following problem as well.
“One animal can run 60 feet in 4 seconds, while another animal can run 100 feet in 8 seconds. Which animal runs faster?” (The first animal runs faster at 15 feet per second.)
Developing the Concept: Rates
Now that students know how to find a unit rate, they will learn how to find an equivalent ratio using unit rates. Finding equivalent ratios uses the same thought process as finding equivalent fractions.
Standard: Use ratio and rate reasoning to find equivalent ratios and solve real-world problems (6.RP.A.3)
- Say: Before we learned how to find a unit rate. Now we are going to learn how to use that unit rate to solve problems. Look at this problem.
- Share the following problem: “Yesterday Ebony ran 18 laps around the track in 12 minutes. If she runs at that rate for 30 laps, how long will it take her?” (Tip: You can substitute the context with anything that would interest your students.)
- Ask: What are we trying to find in this problem?
We are trying to find out how long it takes Ebony to run 30 laps. - Ask: What information do we know that will help us solve this problem?
We know that Ebony can run 18 laps in 12 minutes. We also know she is going to run at that same rate for 30 laps. - Ask: How far does Ebony run in one minute?
Have students try to figure it out individually. Compare student solutions, and discuss why Ebony runs 1.5 laps in one minute. - Say: Let's make a table to list the information we know.
Make the following table but leave "Minutes" blank. Fill it in by soliciting class input.Laps Minutes 1.5 1 3 2 6 4 12 8 18 12 24 16 30 20 - Ask: Does anyone see another way we could have found the time of 20 minutes without writing down the whole table?
Compare the different ideas students offer. Some students might recognize that if they divided 30 by 1.5, they would get 20 minutes. Discuss this strategy with the class. - Write the following problem on the board: “Maria wants to buy a pencil for everyone in her class. It costs $0.78 for 3 pencils. How much would Maria have to spend if she bought a pencil for each of her 24 classmates?”
- Say: I'd like you to solve this problem on your own, and then we'll discuss what you did.
Have students individually share their solutions. Some students may have solved it by finding the unit price or completing a table. Others may have solved it by noticing that 3 pencils cost $0.78, and 24 = 3 × 8. So they multiplied $0.78 by 8 to get $6.24.
***
Looking for more free math lessons and activities for elementary school students? Be sure to explore our Free Teaching Resources hub.
If you're in the market for a math curriculum that will unlock learning for students who struggle with mathematics, check out Math 180, our math intervention solution for Grades 5–12.
Get our FREE guide "Optimizing the Math Classroom: 6 Best Practices."
Related Reading

Eighth graders enjoy a light moment in Alison Van Dyke's ELA class at Valleywood Middle School in Kentwood, Michigan.
















