Number theory, or the study of integers (the counting numbers 1, 2, 3..., their opposites –1, –2, –3..., and 0), has fascinated mathematicians for years. Prime numbers, a concept introduced to most students in Grades 4 and up, are fundamental to number theory. They form the basic building blocks for all integers.
A prime number is a counting number that only has two factors, itself and one. Counting numbers which have more than two factors (such as 6, whose factors are 1, 2, 3, and 6), are said to be composite numbers. The number 1 only has one factor and usually isn't considered either prime or composite.
- Key standard: Determine whether a given number is prime or composite, and find all factors for a whole number. (Grade 4)
Why Do Prime Factors Matter?
It's the age-old question that math teachers everywhere must contend with. When will I use this? One notable example is with cryptography, or the study of creating and deciphering codes. With the help of a computer, it is easy to multiply two prime numbers. However, it can be extremely difficult to factor a number. Because of this, when a website sends and receives information securely—something especially important for financial or medical websites, for example—you can bet there are prime numbers behind the scenes. Prime numbers also show up in a variety of surprising contexts, including physics, music, and even in the arrival of cicadas!
There is another place where prime numbers show up often, and it's easy to overlook when discussing applications: math! The study of pure mathematics is a topic that people practice, study, and share without worrying about where else it might apply, similar to how a musician does not need to ask how music applies to the real world. Number theory is an extremely rich topic that is central to college courses, research papers, and other branches of mathematics. Mathematicians of all stripes no doubt encounter number theory many times along their academic and professional journeys.

Writing a Product of Prime Factors
When a composite number is written as a product of all of its prime factors, we have the prime factorization of the number. For example, we can write the number 72 as a product of prime factors: \(72=2^3 \cdot 3^2\). The expression \(2^3 \cdot 3^2\) is said to be the prime factorization of 72. The Fundamental Theorem of Arithmetic states that every composite number can be factored uniquely (except for the order of the factors) into a product of prime factors. What this means is that how you choose to factor a number into prime factors makes no difference. When you are done, the prime factorizations are essentially the same.
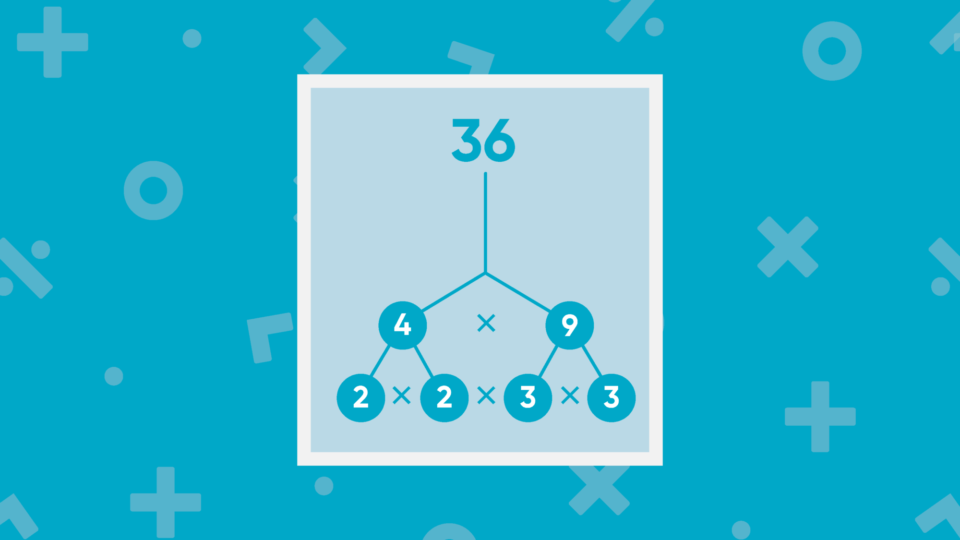
Examine the two factor trees for 72 shown below.

When we get done factoring using either set of factors to start with, we still have three factors of 2 and two factors of 3, or \(2^3 \cdot 3^2\). This would be true if we had started to factor 72 as 24 times 3, 4 times 18, or any other pair of factors for 72.
Knowing rules for divisibility is helpful when factoring a number. For example, if a whole number ends in 0, 2, 4, 6, or 8, we could always start the factoring process by dividing by 2. It should be noted that because 2 only has two factors, 1 and 2, it is the only even prime number.
Another way to factor a number other than using factor trees is to start dividing by prime numbers:
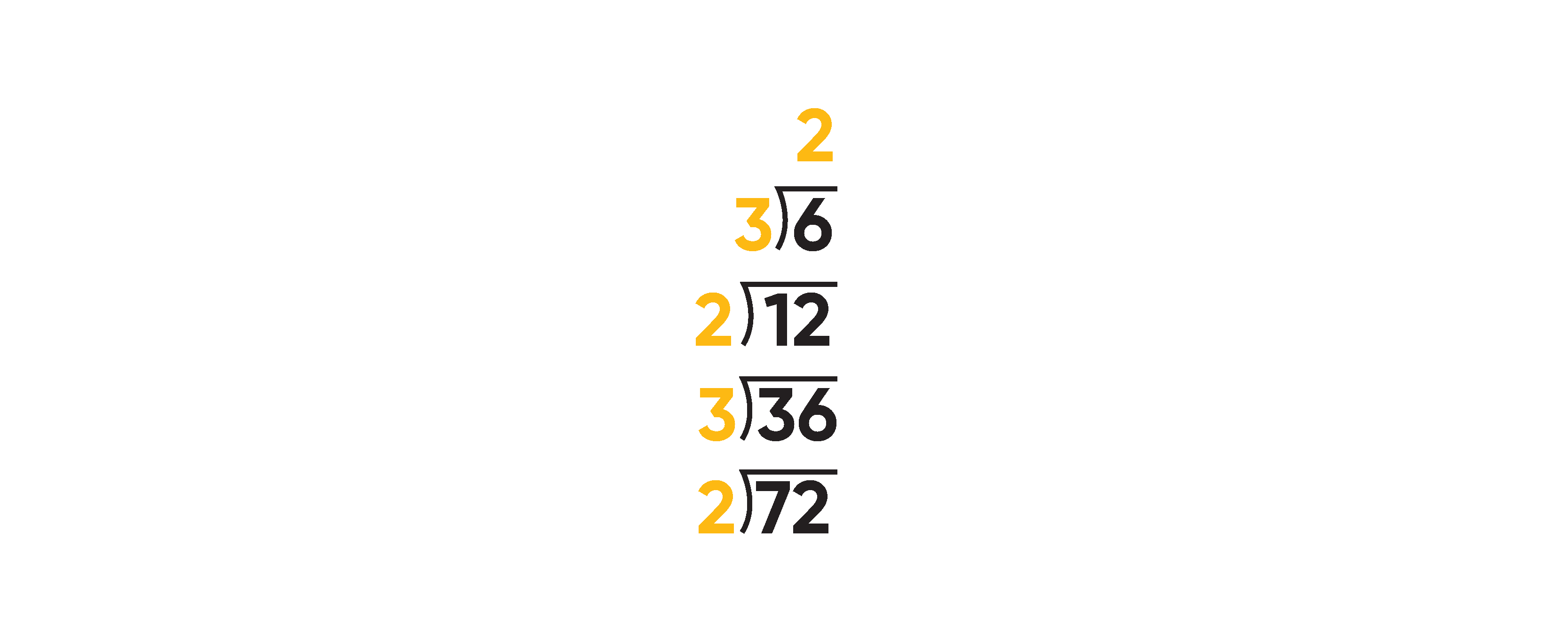
Once again, we can see that \(72=2^3 \cdot 3^2\).
Also key to writing the prime factorization of a number is an understanding of exponents. An exponent tells how many times the base is used as a factor. In the prime factorization of \(72=2^3 \cdot 3^2\), the 2 is used as a factor three times and the 3 is used as a factor twice.
There is a strategy we can use to figure out whether a number is prime. Find the square root (with the help of a calculator if needed), and only check prime numbers less than or equal to it. For example, to see if 131 is prime, because the square root is between 11 and 12, we only need to check for divisibility by 2, 3, 5, 7, and 11. There is no need to check 13, since 132 = 169, which is greater than 131. This works because if a prime number greater than 13 divided 131, then the other factor would have to be less than 13—which we're already checking!
Introducing the Concept: Finding Prime Factors
Making sure your students' work is neat and orderly will help prevent them from losing factors when constructing factor trees. Have them check their prime factorizations by multiplying the factors to see if they get the original number.
Prerequisite Skills and Concepts: Students will need to know and be able to use exponents. They also will find it helpful to know the rules of divisibility for 2, 3, 4, 5, 9 and 10.
Write the number 48 on the board.
- Ask: Who can give me two numbers whose product is 48?
Students should identify pairs of numbers like 6 and 8, 4 and 12, or 3 and 16. Take one of the pairs of factors and create a factor tree for the prime factorization of 48 where all students can see it.

- Ask: How many factors of two are there? (4) How do I express that using an exponent?
Students should say to write it as \(2^4\). If they don't, remind them that the exponent tells how many times the base is taken as a factor. Finish writing the prime factorization on the board as \(2^4 \cdot 3\). Next, find the prime factorization for 48 using a different set of factors. - Ask: What do you notice about the prime factorization of 48 for this set of factors?
Students should notice that the prime factorization of 48 is \(2^4 \cdot 3\) for both of them. - Say: There is a theorem in mathematics that says when we factor a number into a product of prime numbers, it can only be done one way, not counting the order of the factors.
Illustrate this concept by showing them that the prime factorization of 48 could also be written as \(3 \cdot 2^4\), but mathematically, that's the same thing as \(2^4 \cdot 3\). - Say: Now let's try one on your own. Find the prime factorization of 60 by creating a factor tree for 60.
Have all students independently factor 60. As they complete their factorizations, observe what students do and take note of different approaches and visual representations. Ask for a student volunteer to factor 60 for the entire class to see. - Ask: Who factored 60 differently?
Have students who factored 60 differently (either by starting with different factors or by visually representing the factor tree differently) show their work to the class. Ask students to describe similarities and differences in the factorizations. If no one used different factors, show the class a factorization that starts with a different set of factors for 60 and have students identify similarities and differences between your factor tree and other students'. - Ask: If I said the prime factorization of 36 is 22 • 9, would I be right?
The students should say no, because 9 is not a prime number. If they don't, remind them that the prime factorization of a number means all the factors must be prime and 9 is not a prime number.
Place the following composite numbers on the board and ask them to write the prime factorization for each one using factor trees: 24, 56, 63, and 46.
Developing the Concept: Product of Prime Numbers
Now that students can find the prime factorization for numbers which are familiar products, it is time for them to use their rules for divisibility and other notions to find the prime factorization of unfamiliar numbers. Write the number 91 on the board.
- Say: Yesterday, we wrote some numbers in their prime factorization form.
- Ask: Who can write 91 as a product of prime numbers?
Many students might say it can't be done, because they will recognize that 2, 3, 4, 5, 9 and 10 don't divide it. They may not try to see if 7 divides it, which it does. If they don't recognize that 7 divides 91, demonstrate it for them. The prime factorization of 91 is \(7 \cdot 13\). Next, write the number 240 on the board. - Ask: Who can tell me two numbers whose product is 240?
Students are likely to say 10 and 24. If not, ask them to use their rules for divisibility to see if they can find two numbers. Create a factor tree for 240 like the one below.

- Ask: How many factors of two are there in the prime factorization of 240? (4) Who can tell me how to write the prime factorization of 240? (24 • 3 • 5)
Facilitate a discussion around different ways to factor 240 and the pros and cons of each method. If you start with 2 and 120, you end up with the same prime factorization in the end, but you end up with a "one-sided tree" that some students may find more difficult to work with. Have students identify ways that they prefer to factor and guide them to explain their reasoning. - Say: Since the prime factorization of 240 is 24 • 3 • 5, the only prime numbers which divide this number are 2, 3 and 5. Prime numbers like 7 and 11 will not divide the number, because they do not appear in the prime factorization of the number.
Write the number 180 on the board.
- Ask: What two numbers might we start with to find the prime factorization of 180? What other numbers could we use?
Encourage students to find a variety of pairs, such as 10 and 18 or 9 and 20. If no one mentions either pair, suggest them both as possibilities. Have half the students use 10 and 18 and the other half use 9 and 20. Have two students create the two factors for the class to see.
- Ask: If the prime factorization of a number is 22 • 5 • 7, what can you tell me about the number?
- Ask: If the prime factorization of a number is 33 • 11, what can you tell me about this number?
Repeat the previous exercise with a new number. Some possible observations: Because \(3^2\) is a factor, the number is divisible by 9 and the sum of the number's digits is a multiple of nine. Because the product of odd numbers is always odd, the number is an odd number. They might also tell you that it is a composite number, five is not a factor of the number, and so on.
Give them the following numbers and ask them to find their prime factorization: 231, 117, and 175. Also give the following prime factorizations of numbers and ask them to write down at least two things they know about both the number represented: \(3^2 \cdot 5^2\), \(2^3 \cdot 3 \cdot 13\), and \(2^2 \cdot 3 \cdot 5\). You can of course adjust both the numbers and factorizations to match what your students are ready for.
Wrap-Up and Assessment Hints
Finding the prime factorization of numbers will strengthen your students' basic facts and understanding of multiplication. Students who do not know their basic multiplication facts will likely struggle with this, because they do not recognize products such as 24 or 63 readily. Turning the problem around and giving them the prime factorization of a number and asking them what they know about the number without multiplying it out is a good way to assess their understanding of the divisibility rules, the concept of factoring, and multiplication in general.
***
To develop students' conceptual understanding and help them grow into procedurally fluent mathematicians, explore HMH Into Math, our core solution for K–8 math instruction.












