
For students in Grades 3 and up, the leap from multiplication to division can be hard! This article explains what division is, along with the different parts of a division problem (quotient, divisor, and dividend) and how to use the standard algorithm for division. Included are two lessons to introduce and develop the concept to your students. Both lessons are designed to practice fluently dividing multi-digit numbers using the standard algorithm, a standard common in Grades 5–6.
Comparing Division and Multiplication
In order to teach division, it usually helps to start with multiplication. The mathematical expression 3 × 5 represents three groups with five items in each group. To find the product, students can build a model of three groups with five items in each group as shown below.

Students can also use repeated addition to find the product. They can add 3 five times: 3 + 3 + 3 + 3 + 3 = 15.
Remember that multiplication “undoes” division and division “undoes” multiplication. In other words, since 3 × 5 = 15, then 15 ÷ 5 = 3 (and similarly, 15 ÷ 3 = 5). Because division and multiplication are inverse operations, students can use similar models to represent both operations. In the expression 15 ÷ 3, you begin with fifteen items and want to know how many groups you can make with three items in each group. You can see below that this results in 5 groups.

Because multiplication is a form of repeated addition, it follows that division is a form of repeated subtraction. For example, 15 ÷ 3 asks you to repeatedly subtract 3 from 15 until you reach zero: 15 – 3 = 12 – 3 = 9 – 3 = 6 – 3 = 3 – 3 = 0.
Dividend vs. Divisor
This process required 3 to be subtracted 5 consecutive times, so again we see that 15 ÷ 3 = 5. The number that is being divided (in this case, 15) is called the dividend, and the number that it is being divided by (in this case, 3) is called the divisor. The result of the division is the quotient. Notice how you can always switch the divisor and quotient and still have a true equation:
- 15 ÷ 3 = 5
- 15 ÷ 5 = 3

The Standard Algorithm for Division
As students master their basic division facts, the need will arise for students to learn how to divide larger dividends. This is where division earns its reputation for being so difficult! Different sources will offer different ways of thinking about division and solving division problems. American adults are most familiar with the standard long division algorithm, which is explained and used in the lessons here.
It would be prudent to begin with 2-digit dividends and 1-digit divisors, as students are likely to already know many quotients in order to check their work. Then you can progress to larger numbers. Look at the division problem below.

It is sometimes helpful to think of a division problem as a multiplication problem. The above problem can be written as 306 ÷ 6 = ? or ? × 6 = 306.
In the multiplication problem ? × 6 = 306, 306 is the product, 6 is a factor, and ? is a missing factor. That means that in the division problem 306 ÷ 6 = ?, 306 can be thought of as the product, 6 as a factor, and ? as the missing factor. The missing factor is equivalent to the quotient of a division problem. In other words, when looking at 306 ÷ 6, we are trying to find what number multiplied by 6 will give us 306. Understanding this concept will significantly help students learn the long division algorithm.
Begin the long division algorithm by writing the dividend inside the division symbol and the divisor outside it, to the left. The quotient will go on top. Because the 3 is in the hundreds place, begin by asking, "What number times 6 is less than or equal to 300?" Since 5 tens times 6 is exactly 300, a 5 can be written above the 0 in the tens place.
Since 5 tens = 50, and 50 × 6 = 300, we can take 300 away from 306 leaving 6. The process is repeated by asking, "What number times 6 is less than or equal to 6?" Since 1 times 6 is exactly 6, a 1 is written above the 6 in the ones place. Now, because 6 × 1 = 6, 6 is taken away from 6 leaving 0 and completing the division.

Lesson 1: Introducing the Concept of Division
As with addition, subtraction, and multiplication, students practice strategies and algorithms that allow them to perform operations beyond basic facts. After students learn their basic division facts and the concept of division, show them the standard algorithm that they are likely to encounter outside of school.
By Grade 6, most students should be fluent in dividing multi-digit numbers using the standard algorithm. But no matter the grade, remind students that there are many ways to think about division, just like there are many ways to think about multiplication, and this algorithm is one tool to help solve math problems.
Materials: Base-ten blocks that all students can see (for example, with an overhead projector); base-ten blocks that students can use
Preparation: Be sure to provide at least one set of base-ten blocks for each pair of students.
Prerequisite Skills and Concepts: Students should know their basic division facts and have used or seen the use of base ten blocks. Introduce students to the vocabulary dividend, divisor, and quotient prior to the lesson.
- Ask: What does 54 represent in 54 ÷ 9?
54 ÷ 9 is asking: if you have 54 items and divide them into groups with 9 items in each group, how many groups would you have? The 54 represents the total number of items you begin with. - Ask: What does 9 represent in 54 ÷ 9?
The 9 represents how many items are in each group. - Ask: What is 54 ÷ 9?
The quotient is 6. - Ask: What does 6 represent for 54 ÷ 9?
It is the quotient, but more importantly, the 6 represents the number of groups you will divide the 54 items into groups to have 9 items in each group. - Say: Another way to write 54 ÷ 9 is by drawing the long division symbol, placing 54 "inside" it, and 9 to the left. 54 is the total number of items you begin with, and 9 is the number of items in each group. The quotient, or number of groups, is written above the 54:
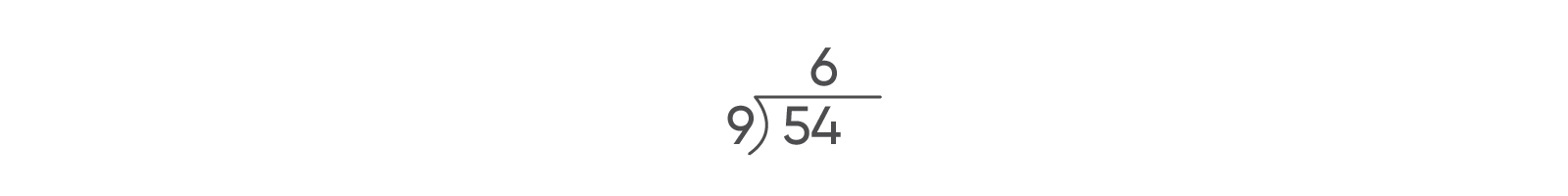
- Ask: Let's try another problem now. What does 68 represent in 68 ÷ 4?
68 ÷ 4 is asking: if you have 68 items and divide them into groups with 4 items in each group, how many groups would you have? The 68 represents the total number of items you begin with. - Ask: What does 4 represent in 68 ÷ 4?
The 4 represents how many items are in each group. - Ask: What is 68 ÷ 4?
Since this is not a basic division fact, it is unlikely that students will be able to find a correct quotient. If students do think they know the quotient, have them share their thinking. Compare strategies, and share that one common strategy for performing more complicated division with multi-digit numbers is using the standard algorithm. - Ask: If we want to write 68 ÷ 4 the same way we wrote the standard long division express "54 divided by 9," what number would go where 54 is and what number would replace 9?
68 would go in place of 54 and 4 in place of 9. - Say: When we are dividing numbers too large for us to immediately know the answer to, it is best to do the problem in several small parts.
- Say: When completing the long division expression "68 divided by 4," remember that 68 is 6 tens and 8 ones.
- Show 6 tens so that the entire class can see them.

- Ask: How many equal groups of 4 tens can you make?
You can make 1 group that will contain 4 tens. - Say: Since you can make only 1 group, you write a 1 over the tens place in 68.
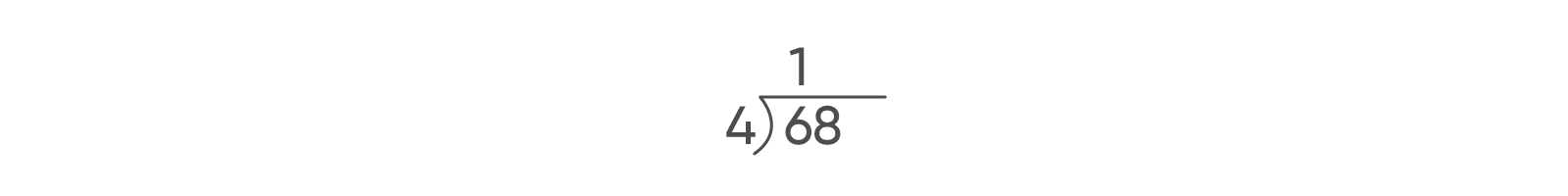
- Say: Since you cannot make additional groups containing four tens, you will need to regroup the remaining 2 for 20 ones.
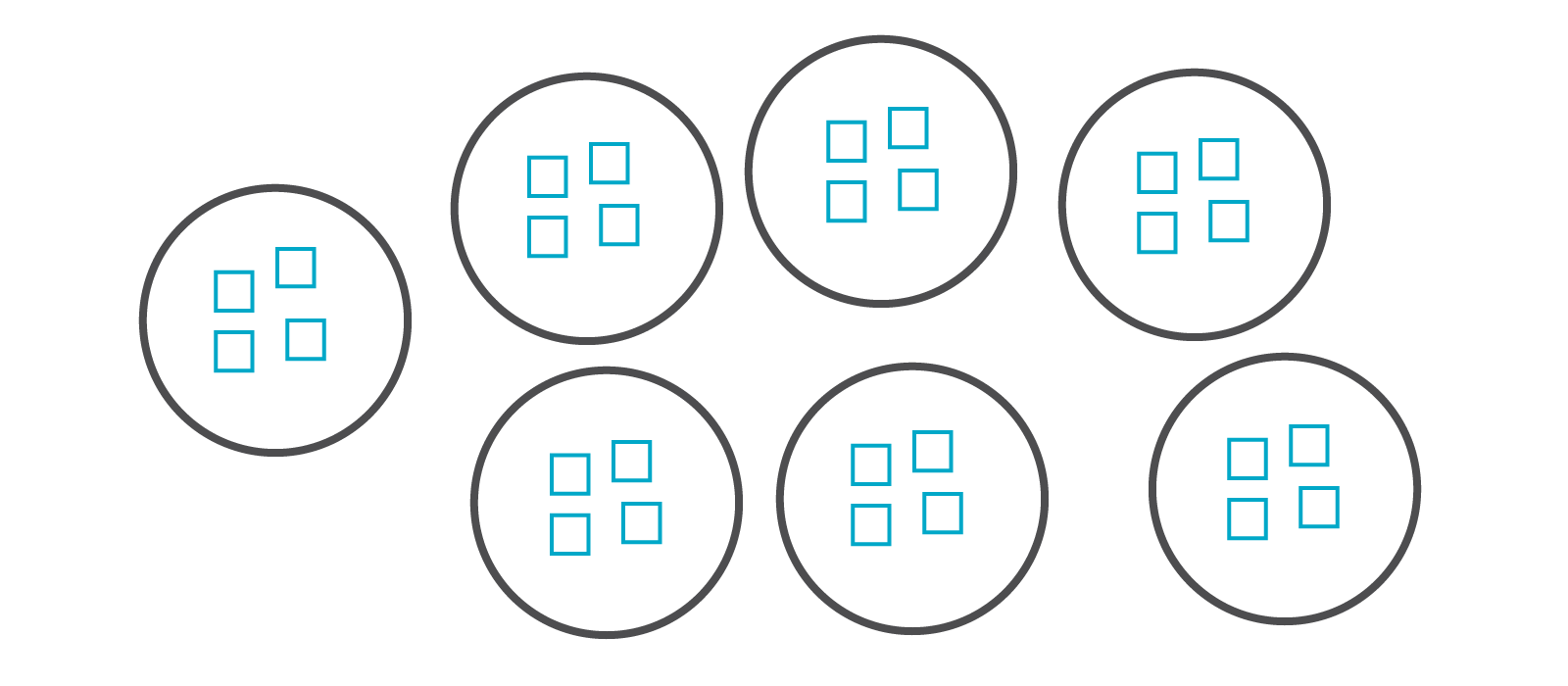
- Show 2 tens being regrouped as 20 ones so that the entire class can see. Next, combine the 20 ones with the 8 ones.
- Ask: If we combine the 20 ones with the 8 ones, how many ones will we have?
28 ones. - Ask: How many groups with 4 ones in each group can we make from the 28 ones?
We can make 7 groups with 4 ones in each group.
- Say: Since 7 groups of 4 ones can be made, we write 7 above the ones place in 68.
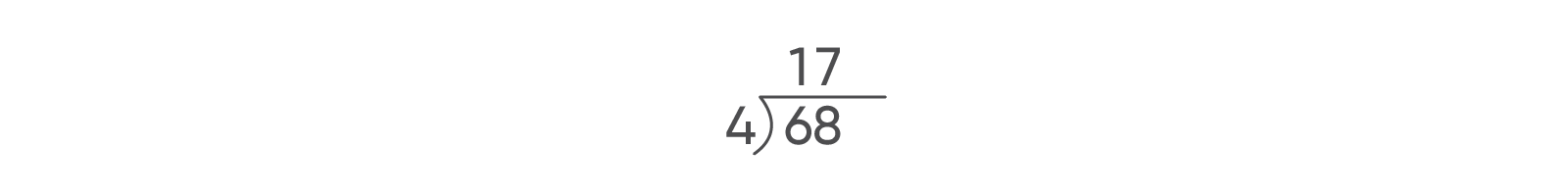
- Say: Since there are no ones remaining, our quotient is 17. If we make 17 groups with 4 items in each group, we should have a total of 68 items.
- Have students individually or in pairs make 17 groups with 4 items in each group. Then have them count the total number of items to see if there are indeed 68.
- Continue this activity using slightly larger numbers. Have the students use their base-ten blocks to determine the place value for the quotient. Remember to always have the students check their work using their base-ten blocks.
Lesson 2: Developing the Concept of Division
After using manipulatives to introduce the division algorithm for multi-digit numbers, it's time to develop the concept more fully. Do not rush the development of this concept. Many students struggle with division of multi-digit numbers, and it is important to allow students plenty of time to master it.
Materials: Base-ten blocks that all students can see (for example, with an overhead projector); base-ten blocks that students can use
Preparation: Be sure to provide at least one set of base-ten blocks for each pair of students.
- Ask: How can we write 276 divided by 6?
276 ÷ 6 or the long division expression with 276 inside the long division symbol and 6 outside it will probably be the two notations used by the students. Encourage students who try different representations, such as the fraction 276/6 or a drawn visual model. - Ask: Which notation will you use to find the quotient of 276 divided by 6?
Direct students to use the long division expression to enable them to use the division algorithm. - Say: Use your base-ten blocks to represent 276.
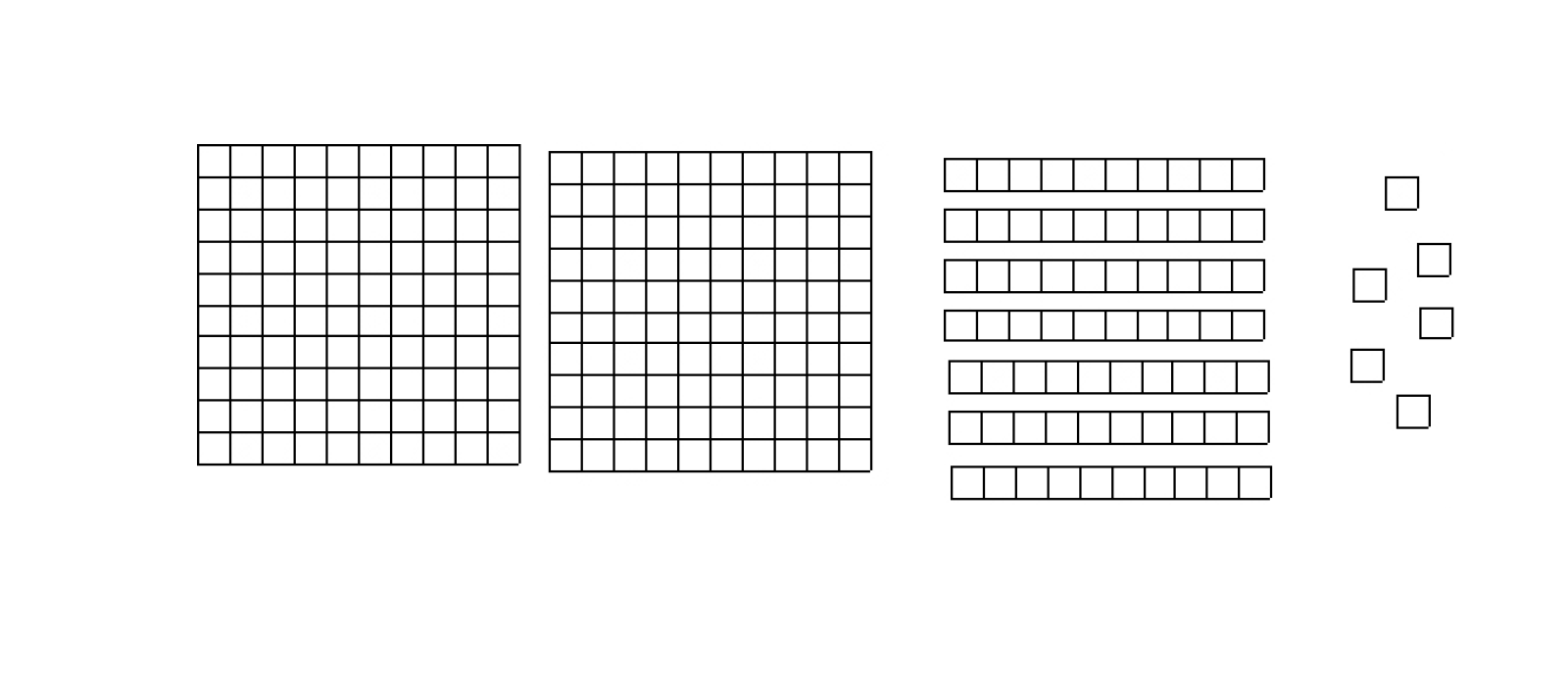
- Ask: Let's begin with the hundreds. Since we are dividing by 6, we need to make groups containing 6 hundreds. Can this be done if we only have 2 hundreds?
No. When you cannot make groups from the current place, you will need to regroup and make groups from the next place. - Ask: If we regroup the 2 hundreds for tens, how many tens would we get? If we include the 7 tens, how many tens would that be altogether?
2 hundreds is equivalent to 20 tens. If we combine the 20 tens with 7 tens, we get 27 tens. - Ask: Since we are working with tens now, how many groups of 6 tens can we make from 27 tens? Be sure to use your base ten blocks.
Notice that there are 4 groups of 6 tens with 3 tens left over.
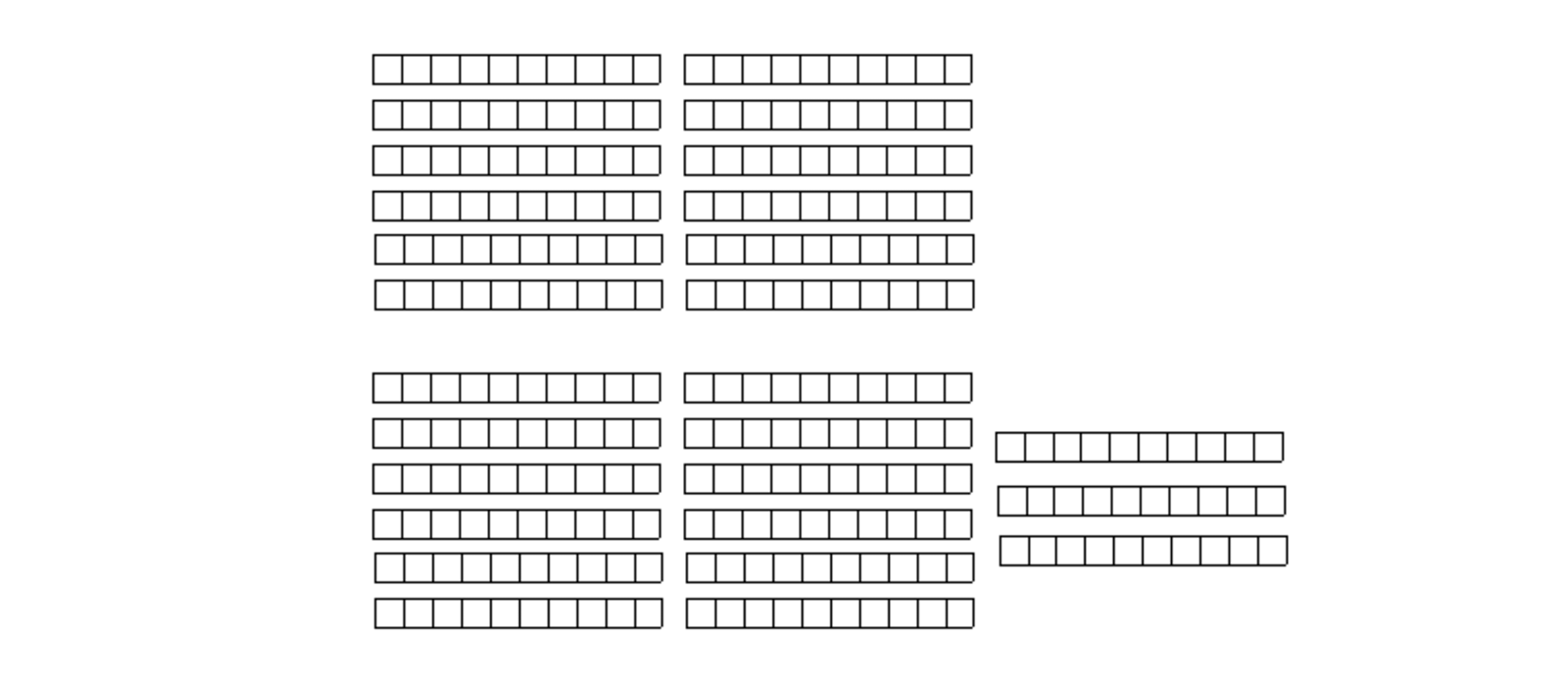
- Say: Since we have 4 groups of 6 tens, we place a 4 over the tens place in 276.
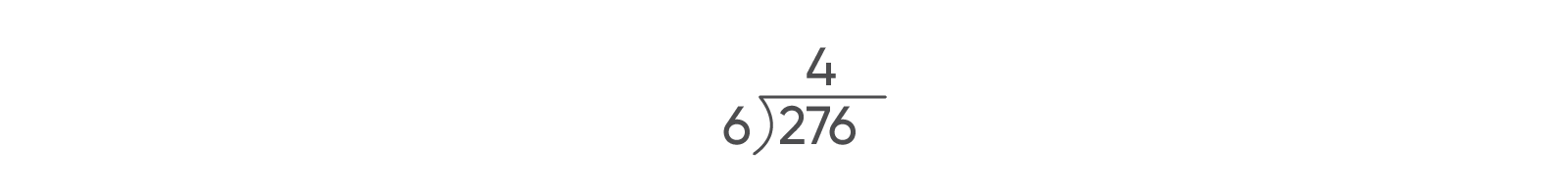
- Ask: If one group of 6 tens is 60, what is 4 groups of 6 tens worth?
240. Encourage students to use their base-ten blocks to illustrate the value. - Say: Remember that we began with 276 and want to divide it by 6. Since we have made four groups, each with 6 tens, we can take 240 away from 276.
- Ask: How many tens and ones are left over when we take away the 4 groups of 6 tens?
3 tens and 6 ones are left over. - Say: We can do this by writing 240 below 276 in our division problem and subtracting.
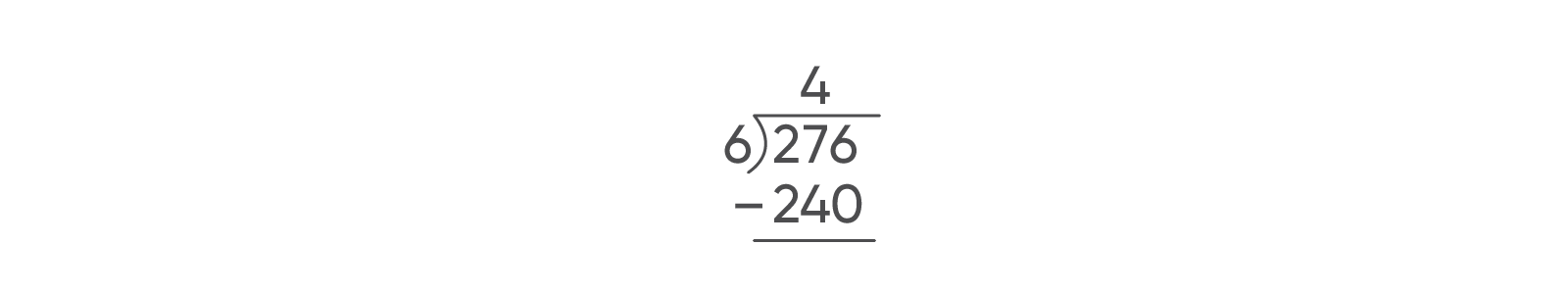
- Ask: What is 276 – 240? What is the value of the base-ten blocks that you have left over? What do you notice about the two values?
36. This helps students see the connection between using the base-ten blocks and the standard algorithm. - Ask: Since we cannot make any more groups of 6 tens with the remaining base-ten blocks, we can regroup the 3 tens for how many ones?
30 ones. In front of the students, regroup 3 tens as 30 ones. - Ask: How many ones do we now have?
We have 36 ones. - Ask: How many groups of 6 ones can we make from 36 ones?
We can make 6 groups. - Ask: Where do you think we will write the 6 that represents the 6 groups?
The 6 is written above the ones place in 276. - Ask: Are there any ones left over?
No. - Ask: What is the quotient of 276 ÷ 6?
46 - Continue this activity using different numbers. Be sure to use numbers that do not use remainders at first. To reinforce the connection between multiplication and division, have students check their work using multiplication.
Wrap-Up and Assessment Hints
Students need a great deal of practice when learning to divide multi-digit numbers. Do not be in a rush for students to put away their manipulatives when learning this difficult concept. This can be a trying time in many students' mathematical development!
As a teacher, do not be discouraged by slow progress. Remember, this may be the first time many of your students have ever encountered the concept. Your task is to take the needed time and effort to encourage students to learn this process. As much as possible, try to relate different division problems to your students. If they're interested in basketball, for example, have them divide groups of players or basketballs. Additionally, connect division to other topics, such as multiplication, fractions, and equations, when they appear to reinforce the concept many times.
Continual assessment when teaching division is necessary and can take the form of warm-up problems, digital practice (for example with our own digital math practice solution, Waggle), or exit tickets, in addition to more formal assessment such as quizzes and tests. Return to the concept throughout the year to ensure retention and build mastery.
***
Need more ideas to teach what is a divisor in math? Looking for more free lessons and activities for elementary and middle school? Be sure to explore our Free Teaching Resources hub!
Hear one teacher’s vision of rhyming and rhythms for teaching division beyond algorithms.












